Theory
Airway Generation
Airway Generation
For each airway insonification model we create, a set of airways has to be generated. In this section, we will discuss how this happens
CT Segmentation
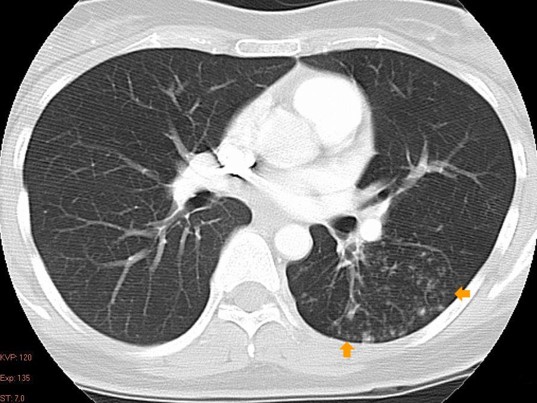
Figure 1
CT Segmentation
CT/MRI Segmentation is widely used in a clinical setting, and it generates airways through image processing techniques. This process is called image segmentation. Image segmentation has the benefit of generating anatomically accurate geometry up to the resolution of the picture, and can be generated relatively quickly, depending on the quality of the CT/MRI pictures. Small airway segments, down to a few millimeters, however, cannot be segmented easily (if at all).
This is the most widely used means as generation of the airways. This is done through creating a digital geometry of the airways via CT or MRI imaging: airways are traced through contrast differences. In figure 1 shown to the right, you can see an example MRI/CT image.
CT Segmentation Continued
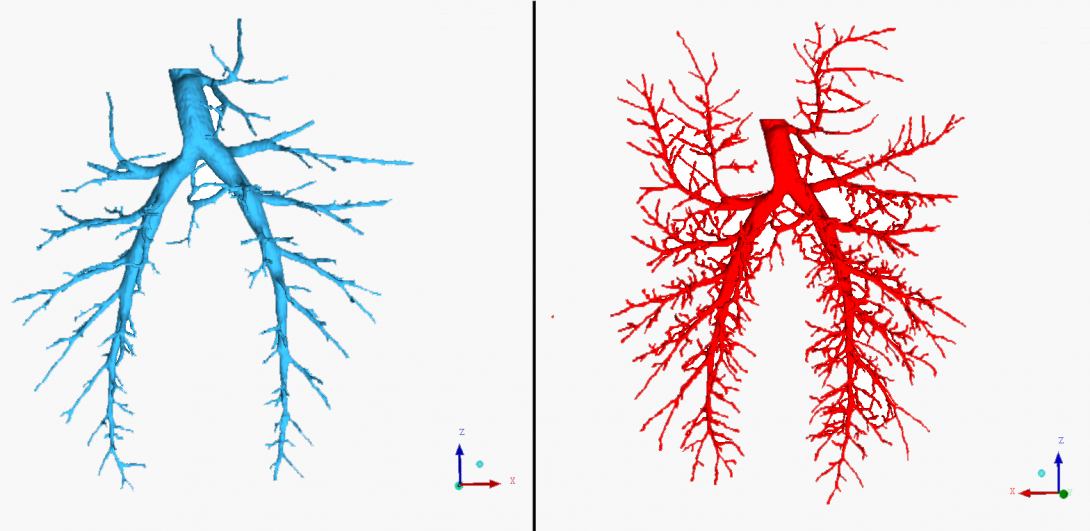
Figures 2 (left) and 3 (right)
Applications like ITK/SNAP are then used to trace the shown white contrast and save the data as a stereo lithographic (STL) file. This is computer-aided design (CAD) file of the airways. An example of a traced airway can be seen to the left in Figures 2 and 3.
Airway Generation through Algorithmic Means
Airway Generation through Algorithmic Means
This next segment will go into new means of generating airway geometry algorithmically. Generating airways algorithmically means generating them through computer code rather than through image processing. This has a couple of benefits: it can be very fast, and depending on the code, can produce highly relevant (it looks very similar to real airways) airways. However, some of the patient-specific differences in structure can be lost.
Airway Generation: Hiroko Kitaoka’s Code


Figures 4 (left) and 5 (right)
These are some airway trees generated through a collaborators code. Shown in Figures 4 and 5 are a very detailed (around 55 thousand airway segments) tree. It was grown to produce a highly relevant airway geometry for a given set of boundaries (in this case, a digital lung geometry given by constraint equations).
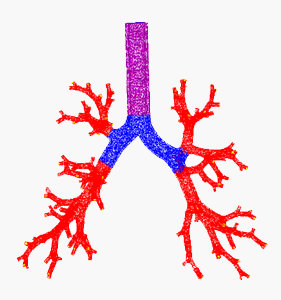

Figures 6 (left) and 7 (right)
Shown in Figures 6 and 7 is another airway geometry, with a much lower order of complexity, but is shown with a layer of thickness surrounding the airway segments. Airways are typically surrounded by cartilage, and this cartilage thickness can be programmatically preserved as well.
These airways can be generated in a matter of minutes, and can reach a level of complexity far greater than image segmentation can reach. It can grow airway segments down to the alveolar level, which is sub millimeter in diameter.
Airway Generation: Constrained Constructive Variant
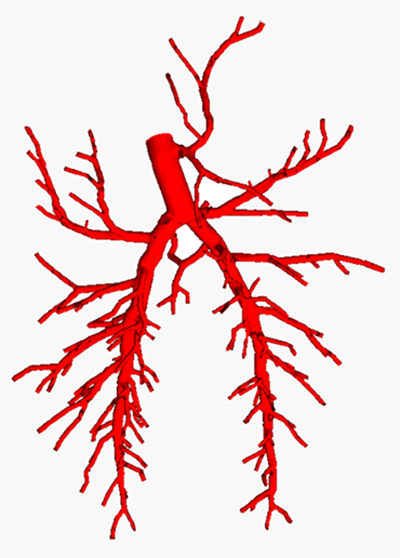
Figure 8
Airway Generation: Constrained Constructive Variant
The last programmatic means the Audible Human Project team is investigating is generating airways through a variant of the Constrained Constructive Optimization (CCO) algorithm.
CCO grows airway trees on a segment by segment basis, optimizing the volume of the tree with each iteration. Segments are grown on a quasi-random basis, which can provide a few advantages: each model grown is quasi-random. This means that many models can be created from the same geometry.
One final benefit of CCO is that it can be grown on top of a base geometry, which can be provided by CT/MRI imaging. By doing this, you can capture the patient-specific differences in anatomical structure in the airway tree down to a few millimeters, and then use CCO on that tree to grow additional segments down to sub millimeter diameters.
On the left in Figure 8 is a CCO generated airway tree.
Sources
- Kitaoka Information: http://www7b.biglobe.ne.jp/~lung4cer/indexEng.html
- CCO Articles
– Schreiner, Wolfganfg et al (1995). “The Influence of Optimization Target Selection on the Structure of Arterial Tree Models Generated by Constrained Constructive Optimization.” J. Gen. Physiol. 106, 583-599
– Schreiner, Wolfganfg et al (1996). “Structural Quantification and Bifurcation Symmetry in Arterial Tree Models Generated by Constrained Constructive Optimization”. J. Theor. Biol. 180, 161-174
– Karch, Rudolf et al. (1999). “A three-dimensional model for arterial tree representation, generated by constrained constructive optimization.” Computers in Biology and Medicine. 29, 19-38